Bezierlines

A bezierline is drawn as a series of cubic bezier curves and defined by a set of ordered bezier vertices.

A cubic bezier curve is defined by four points; p0, p1, p2 and p3. The cubic bezier curve starts at p0 and heads toward p1 before moving to p3 from the direction of p2.

A bezier vertex consists of three points, p0, p1 and p2. p1 represents the point on the line, while p0 represents the preceeding control point and p2 represents the subsequent control point. Thus, a curve heading into p1 will arrive from the direction of p0 and leave in the direction of p2.

Two bezier vertices, v0 and v1, are needed to define a bezier line segment or curve. This results in a total of six points (three points for each vertex):

    v0p0   v0p1   v0p2   v1p0   v1p1   v1p2

The cubic bezier curve from v0p1 to v1p1 will only use four of these points. It will leave v0p1 heading in the direction of v0p2 and arrive from the direction of v1p0 at v1p1. If you place the points in the previous sentence in the order they are mentioned you get:

           v0p1   v0p2   v1p0   v1p1

which is the same sequence as above.

If this bezier line contained a third vertex, the following points would be present to define the following bezierline segments:

    v0p0   v0p1   v0p2   v1p0   v1p1   v1p2   v2p0   v2p1   v2p2
           |------ segment 1 ------|
                                |------ segment 2 ------|

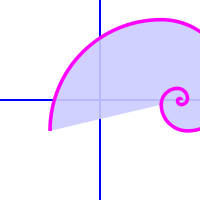
Filled Bezierline

Bezierlines may be filled or unfilled. An unfilled bezierline is more conceptually familiar with what is implied by a bezierline. A filled bezierline is essentially an unclosed beziergon.